The non-linear bicycle model considers longitudinal (x), lateral
(y), and yaw 
motion under the assumption of negligible
lateral weight shift, roll and compliance steer while traveling on
a smooth road. Our design of control strategy is to control both
longitudinal and lateral motions during hard braking and steering
maneuvers. Angular velocities of front and rear tires are added to
the states in order to investigate directional interactions
between longitudinal and lateral tire forces. In addition to these
five states, longitudinal and lateral positions and yaw angle with
respect to the fixed inertial coordinates are added to the dynamic
equation in order to refresh the vehicle position and orientation
in the simulation scene. Thus, the bicycle model used in our
simulator has 5 Degrees Of Freedom with 8 state equations.
The bicycle model developement presented here is based on
reference [1]. Figure 1 shows side and top
views of the vehicle using this bicycle model. Using free body
diagram shown in top view of Figure 1, the equations of motion are derived.
Figure 1: Free Body
Diagram of a Vehicle
Summing the longitudinal forces along the body x axis leads to
Where m is the mass of a vehicle, 
and 
are the
longitudinal and lateral components of the vehicle velocity
resolved along the body axis, r is the yaw rate, and 
and 
are the front and rear wheel steering angles.
Summing the lateral forces along the body y axis gives
The sum of the yaw moments about the car CG yields
Figure 2: Free Body
Diagram of a Wheel
For the front and rear wheels, the sum of the torque about the
axle, as shown in Figure 2, results in
Where, 
and 
are the angular velocities of the
front and rear wheels, 
is the inertia of the wheel about the
axle, 
is the wheel radius, 
and 
are the
applied braking torques, and 
and 
are the applied
throttling torques for the front and rear wheels. All the vehicle
specifications are based on the 1984 Honda Accord [2]
with reasonable braking torques for front and rear tires. Yaw
angle is directly found by integrating the yaw rate. Since yaw
angle is with respect to the fixed coordinates, longitudinal and
lateral position with respect to the inertial fixed coordinates
are also found as follows.
Where, 
and 
denote the velocity components with respect
to the fixed inertial coordinates. Simple integration based on the
forth-order Runge-Kutta method is used to integrate the above eight
states in the simulation loop.
The longitudinal and lateral forces from front and rear tires are
derived from the non-linear tire model discussed earlier. The
input variables for the tire model are front and rear normal loads
(
and
), slip angles (
and
), and longitudinal slip ratios (
and
). The normal forces of front and rear tires are
determined according to the instantaneous longitudinal
acceleration. Summing the moments about the rear contact patch
using the side view of Figure 1, normal load of front
tire is found as
Summing the moments about the front contact patch,
Where
is the instantaneous longitudinal acceleration and h
is the height of the car CG from the ground.
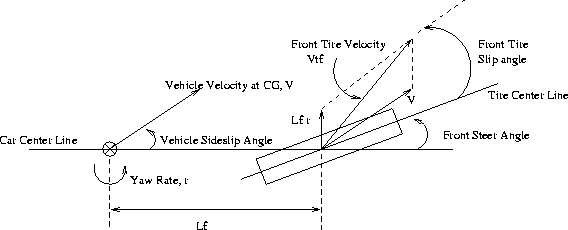
Figure 3: Slip Angle
of Front Wheel
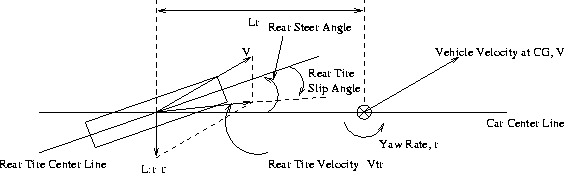
Figure 4: Slip Angle
of Rear Wheel
From Figure 3 and Figure 4, velocities
of front and rear tires are determined by summing the velocity at
CG and the velocities effected by the yaw rate. Thus, the slip
angles of front and rear tires are found as
Also, the speed of the front and rear tires are calculated by the
following equations.
Where,
and
represent the magnitude of the front
and rear tire axle velocities. To calculate the longitudinal slip, longitudinal
component of the tire velocity should be derived. The front and
rear longitudinal velocity components are found by
Then, the longitudinal slip is determined according to the equation in
tire model. Under braking conditions, longitudinal slip of front
and rear tires are calculated by
Using the normal load, slip angle, longitudinal slip, and
non-linear tire model realistic longitudinal and lateral forces
are generated for the 5 DOF bicycle model.
References
- 1
- Taheri, S.,
An Investigation and Design of Slip Control Braking Systems
Integrated with Four Wheel Steering, Ph.D. Thesis, Clemson
University, 1990.
- 2
- American Honda Motor Company Inc.,
Motor Vehicle Specifications, Passenger Car, Accord 1984,
Technical Report, Honda, Windsor Locks, 1984.