As mentioned in the previous text the random variables are practically described by a finite set of moments. It is obvious that a more precise description of the moments yields a more accurate nonlinear filter. The CoDE laboratory is currently involved in the development of higher order unscented filters [5].
To capture higher order moments, the sigma-set is symmetrically expanded, which introduces additional design parameters. The augmented sigma-set is shown in the following figure:

![]()
The augmented sigma-set is capable of matching higher order moments, where the sigma points and the weights are the design variables. Depending on the number m of augmented sigma points, a variable order of moments can be approximated. The two-sigma-set, for example, is capable of matching up to the eighth order moment. In [5] we have shown the solution of the 5 unknowns for the two-sigma-set, which are repeated here:
|
|
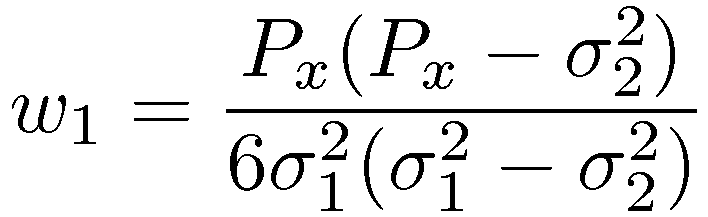 |
||
|
|
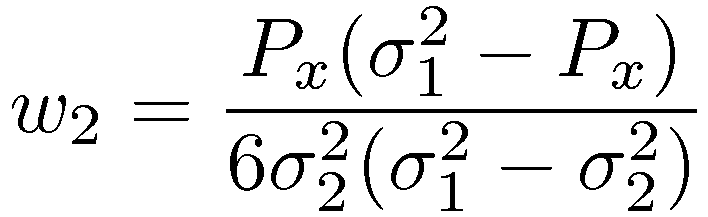 |
(Please note that the weight w2 has been type-set incorrectly in [5].) |
These equations can be further simplified by substituting the sigma-points into the equations of the weights.
|
|
where |
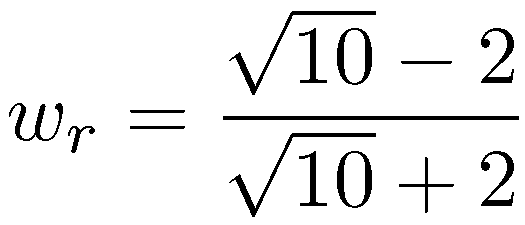 |
||
|
|
The expansion to the 3-sigma-set enables the higher order unscented filter to match up to the twelfth order moment.
| Top of Page |