The standard Unscented Transformation (UKF)

The judiciously chosen samples are called the sigma-set. It is being generated as weighted perturbations from the mean:

Where the perturbations are the columns of the matrix square root of the covariance matrix Px:

The statistics of the sigma set are determined by the weighted sum as indicated in the following equation:

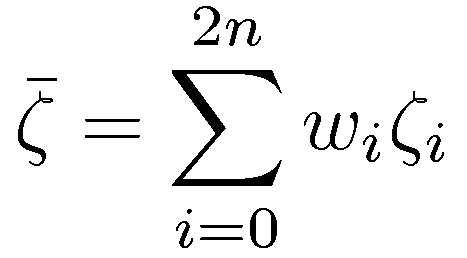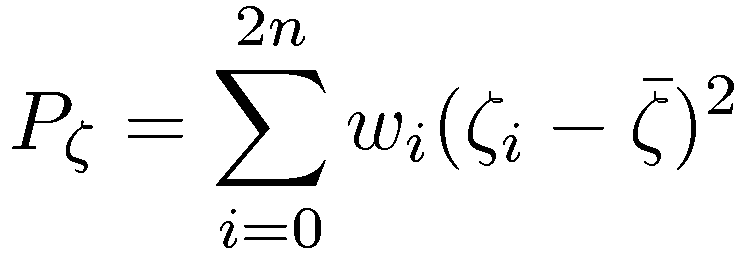Note that the moments are called statistics and can be calculated with the knowledge of the pdf. A random variable can be fully described by its pdf or an infinite set of moments. In most applications the random variable is described by the first two moments, i.e. the mean and variance. It is therefore an approximation of the statistics of the random variable. The extended Kalman filter matches the transformed statistic up to the first order and the unscented filter matches up to the second order (in the special case of symmetric distributions up to the third order and for appropriate choices of kappa up to the fourth order moment). However the weights are obtained by equating the statistics of the sigma-set to the statistics of X.

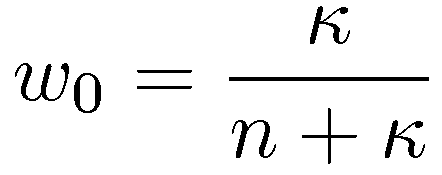
The standard unscented transformation is a symmetric set, which requires at least 2n points. This is in 2D we need 4 points to describe the covariance ellipse. However 2n+1 samples are used to provide an additional design parameter kappa, which scales the higher order moments. The effect off the sigma-set on the higher order moments are discussed in the following section. Furthermore, the smallest possible sigma-set is defined in the subsequent section.

1. Simon Julier, Jeffrey Uhlmann and  Hugh Durrant-Whyte. New Approach for Filtering nonlinear Systems. In Proceedings of the American Control Conference, Vol. 3, pages 1628-1632, 1995.
2. Simon Julier. Scaled Unscented Transformation. In American Control Conference, May 8-10, Anchorage, Alaska, 2002.
3. Simon Julier. Minimum Skew Unscented Transformation. In American Control Conference, May 8-10, Anchorage, Alaska, 2002.
4. Simon Julier. Spherical Unscented Transformation. In American Control Conference, June 4-6, Denver, Colorado 2003.
5. Dirk Tenne and Tarunraj Singh. The Higher Order Unscented Filter. In American Control Conference, June 4-6, Denver, Colorado 2003.